Теорема Птолемея.
(Клавдій Птолемей II ст. н.е.)
В епоху середньовіччя книга Птолемея „Альмагест”, як називали її астрономи (найвеличніше), мала велике поширення в країнах арабського Сходу. Вона містила широкі відомості з астрономії і математики.
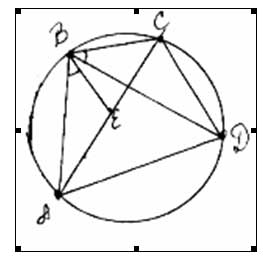
Теорема. Якщо чотирикутник ABCD вписаний, то AB∙CD+BC∙АD=AC∙BD
Доведення
Візьмемо на діагоналі AC таку точку E, що ABE=DBC. Тоді ∆ABE ~ ∆DBC, бо BAE= BAC= BDC.
Тому AB:DB=AE:DC, тобто AB∙DC=AE∙DB. (*)
CBE=DBA, отже, ∆CBE ~ ∆DBA, бо BCE =BDA. Тому CB:DB=EC:DA, тобто CB∙DA=DB∙EC (**).
Додавши почленно рівності * і ** , маємо: AB∙CD+BC∙AD=AC∙BD.
Ця теорема знадобилась олександрійському астроному Птолемею для складання таблиці синусів, точніше таблиці довжини хорд. Якщо AC – діаметр кола, то теорема Птолемея переписується у вигляді
cosα sinβ+sinαcosβ=sin(α+β). Якщо за діаметр взяти сторону AB, то одержимо формулу sin(α-β).
Теорема Птолемея широко використовується для розв’язування задач.
Задача
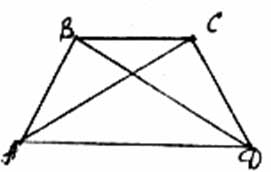
Нехай AD і BC – основи рівнобічної трапеції ABCD.
Довести, що 
Розв’язання.
Так як рівнобічну трапецію завжди можна вписати в коло, то за теоремою Птолемея маємо:
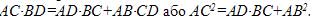
Теорема Чеви
Чева Джованні (1648-1734) – відомий італійський інженер-гідравлік і геометр. Він створив учення про січні, що започаткувало нову синтетичну геометрію.
Теорема. Нехай точки A, B, C, лежать відповідно на сторонах BC, AC, AB трикутника ABC. Відрізки AA1, BB1, CC1 перетинаються в одній точці О всередині трикутника тоді і тільки тоді, коли
(AB1/B1C)∙(СA1/A1B)∙(BC1/C1A) = 1.
Доведення
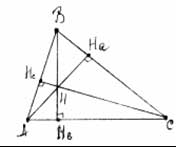
Через вершину С проводимо пряму, паралельну стороні АВ. Точки перетину цієї прямої з прямими АА1 і ВВ1 позначимо відповідно M і N. При гомотетії з центром О і коефіцієнтом k=OC/OC1 точки А, В і С1 відображаються відповідно на точки M,N і С. Отже (AC1/C1B)=(MC/CN).
Трикутники АВА1 і МСА1, АВВ1 і CNB1 гомотетичні. Тому (BA1/A1C)=(BA/MC), (CB1/B1A)=(CN/BA). Перемноживши знайдені три рівності почленно, одержимо (AС1/С1C)∙(СA1/A1B)∙(BC1/C1A) = 1.
Обернену теорему можна довести від супротивного, допустивши, що прямі АА1 і ВВ1 перетинаються в якійсь точці О, а пряма СО перетинає АВ в якійсь точці D. Потім доводимо, що точка D співпадає з точкою С1, використавши для цього пряму теорему.
Застосовуючи теорему Чеви, можна легко розв’язувати задачі на доведення того факту , що висоти, медіани, бісектриси трикутників перетинаються в одній точці.
Задача
Довести, що медіани трикутника перетинаються в одній точці.
Розв’язання.

Нехай АА1, ВВ1 , СС1 – медіани трикутника. Тоді маємо: (АВ1/В1С)∙(СА1/А1В)∙(ВС1/С1А)==1∙1∙1=1.
Твердження доведено